ファインチューニング（３）

前回の投稿（ファインチューニング（２））では、ラベルのみでは区別できないケースがある点にも触れましたが、それでも現時点で最も有効なワインの識別方法がラベルによる識別である点は変わりませんので、もう少し精度の向上を目指したいと思います。

用語の整理

昨今の投稿において、学習用画像データの呼称に関して自分でも混乱しがちなので、改めて整理したいと思います。

まず、広い言い方で「モデルの学習」に使用している画像は全部で200点ですが、狭義の「学習」に該当する「パラメータ（重み）の変動」に関係しているのは160点で、残りの40点は学習結果の検証（val_lossの算出）に使用されるのみです。

また、上記200点は全て異なるラベルの画像になりますが、それ以外に同じラベルを撮影した異なる画像のサンプルとして、「ラベル画像のトリミング（５）」で用意した、各ラベルにつき5点の画像を持つ4セット、計20点の画像が存在します。
現在は、これら画像は最終的な識別精度の確認だけに使用されており、モデルの学習には一切関与していません。

上記のように、画像データは3種類（160点、40点、20点）に分かれるのですが、これらの呼称が結構いい加減でしたので、巷で使用されている用語なども参考にしつつ、今後は以下のように表記したいと思います。

• 訓練（train）データ：学習過程において、パラメータ（重み）の変動に使用されるデータ
• 検証（validation）データ：学習過程において、結果の検証（val_lossの算出）に使用されるデータ
• テスト（test）データ：学習に関与せず、学習済モデルの精度評価にのみ使用されるデータ

なお、「学習用データ」と表現した場合は、訓練＋検証データを意味します。

また、画像の比較において、比較の基準となる画像を「アンカー」、アンカーと同じ対象物を撮影した別画像を「ポジティブ」、アンカーとは異なる対象物を撮影した画像を「ネガティブ」と表現しています。
この呼称は、今回実施しているような距離学習（Metric Learning）で用いられる用語ですが、便利なので今後もこの表現を使用していきます。

改善施策

以下に、今回実施した施策に関して列記します。

施策１：ネガティブリストの数の変更

前回は、各アンカーから距離が近い順に20点の画像でネガティブリストを構成していましたが、もともとハードネガティブとなるように意識して集められた画像ではないため、20点も選択してしまうと、後半の方はハードさがかなり薄れてしまうように思われます。

よって、数を半分の10点とし、合わせてバッチの実行回数も半分の50回としました。

施策２：データ拡張は訓練用ポジティブのみ適用

前回までに実施した学習では訓練データ内のネガティブに対してもデータ拡張を実施していました。
学習パターンの多様性という意味では良い面もあるのかもしれませんが、せっかくアンカーに近いネガティブを選択しておきながら、データ拡張を適用することで距離を遠ざけてしまっては本末転倒と言えます。

よって、訓練データにおいてデータ拡張を適用するのはポジティブのみとしました。
なお、検証データに関しては最初からデータ拡張は適用していません。

施策３：透視変換（RandomPerspective）の実施

データ拡張は大雑把に分けると色合い（明度、彩度等）の操作と構図（被写体の配置や大きさ等）の操作の2種類があります。
構図の方に関してはラベルの位置を微妙に上下左右に動かしたり、拡大・縮小を行なっていましたが、これだとラベルの形状はほとんど変わりません。

一方で、同じラベルを写した異なる画像間で距離が離れていると判断されがちなケースは、以下のようなケースです。

左側は遠くから、右側は近くから撮影した結果、同じラベルを写したものでありながら、右側の方が全体的な歪みが大きいくなっており、見た目の印象がかなり変わっています。

上記のような歪みをそのまま再現することは簡単ではないようですが、元画像を適度に歪ませるだけであれば Keras の機能 RandomPerspective で実現できるようなので、今回からは同操作を追加しています。

具体的には以下のような内容です。

        keras.layers.RandomPerspective(
            factor=(1.0, 1.0),
            scale=0.2,
            interpolation="bilinear",
            fill_value=0.0,
        ),

実は上記関数に関しては情報が少なく、Gemini先生の助言も怪しかったりしたので（PyTorchと混同したりしていましたが）、試行錯誤の結果、上記内容になっています。
正確性に関しては保証の限りではありませんが、一応それっぽく処理できているようでした。

なお、上記操作によりラベルの大きさや位置が微妙に変化するようになったので、内容が重複する RandomZoom（拡大・縮小）と RandomTranslation（移動）は適用しないようにしました。

施策４：データ拡張に色相操作を追加

一方で、データ拡張による色合いの操作に関しては、明度や彩度に関する操作は行なっていたのですが、色相に関する操作は行なっていませんでした。
これは、色相を変化させすぎるとポジティブの識別に支障を来たすとのGemini先生の助言があったためですが、照明の種類などによって色の見え方も結構変わる場合があるので、その辺を考慮して、軽く色相操作を入れてみました。

image = tf.image.random_hue(image, max_delta=0.1)

施策５：検証データの固定化

今までの学習の推移を見ると、val_lossの減衰傾向が明確に確認できたことは、ほぼ無かったと言って良いです。
大体は激しく増減するギザギザの波線になるのですが、これは検証データをランダムに抽出していたことの影響も大きいように思います。

よって、今回からは検証データは固定化し、予め生成されたリストに準じて毎回同じ内容の検証（val_loss算出）が行われるようにしました。

検証の適正化は学習の精度向上に直接関与するものではありませんが、val_lossを学習の早期停止（EarlyStopping）の指標にしていたり、val_lossが最も小さかったモデルを学習の成果として採用する（ModelCheckpoint）と言うことを行なっていたりするので、間接的にはモデルの精度に影響する内容だと思っています。

結果確認（１）

以下に、前述の施策実施結果を示します。

まず、データ拡張によって元画像がどのように変化するかを紹介しておきます。
一番左が元画像で、以降の4点がデータ拡張による変更結果です。

歪みに関しては良い感じで適用されているようです。
色相の変化に関しては控えめですが、あまり派手に変わっても逆に悪影響がありそうなので、この辺が適当かもしれません。

次に学習状況に関して紹介します。

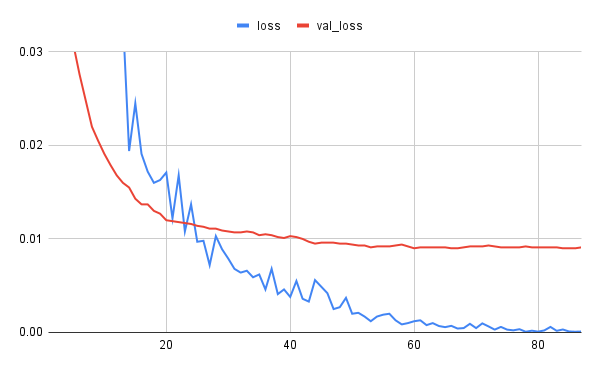
val_lossの推移が劇的に安定しました！
これであれば、減衰途中にあるのか、停滞状態にあるのかが直感的に分かります。

上記学習によって、モデルの精度がどの程度向上したかについても見てみましょう。

まずは、学習用データ内での各アンカーに対する他の画像との最短距離の変化を確認します。

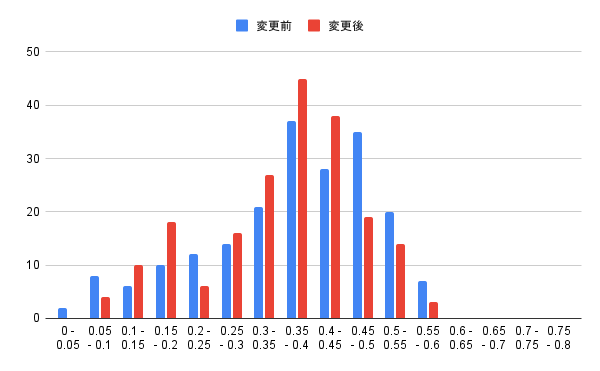
全体的には大きくは変化していませんが、ポジティブ認定域である0.15未満辺りの状況は良くなっているようです。

テストデータに関するポジティブ、ネガティブの分布状況に関しても見てみましょう。

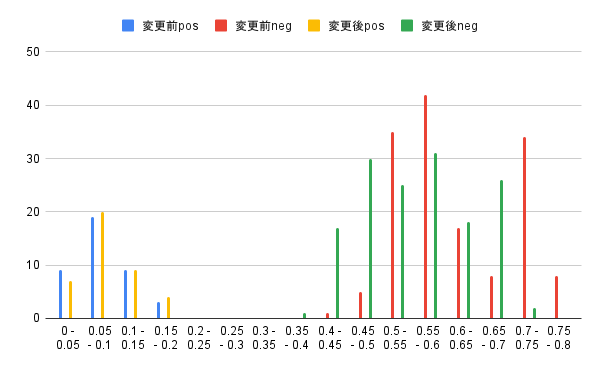
こちらは、あまり改善が見られません。
ネガティブの分布に関しては、むしろ距離が近づいている（精度的に劣化している）ようにも見えます。

結果全体を見た印象としては、val_lossの推移が安定したことを除けば、施策の効果はかなり限定的であったと言わざるを得ないようです。
1回の学習結果だけで結論を出すのは早計かもしれませんが、もう少し根本的な部分で改革が必要な気がします。

訓練可能（trainable）レイヤの調整

と言うことで、「もう少し根本的な部分」の一つである、訓練可能なレイヤの選択に関して見直してみたいと思います。

現在は「conv5_block1_out」なるレイヤ以降を訓練可能としています。
この点に関してはGemini先生のお勧めであったと言うのが唯一の理由ですが、一方で現状の閉塞感に関しても相談してみたところ、「チューニング可能なレイヤーをもう少し前まで含めることで、精度が上がる可能性は十分にあります」とのお墨付きをもらったので、改めて訓練可能レイヤを変更して、状況を確認してみたいと思います。

では、どのレイヤを選択するかに関してですが、例によってGemini先生の、

conv5_block1_outからconv4_block1_out、次にconv3_block1_outといったように、チューニング可能な範囲を段階的に広げて、それぞれの設定でモデルの性能（特に検証損失）を比較します。

と言うアドバイスに従って、「conv4_block1_out」と「conv3_block1_out」を試してみることにします。

結果確認（２）

まず、ResNet50のパラメータは全部で23,587,712個あるようですが、訓練可能なレイヤの指定を変えることで、訓練可能なパラメータ数や学習に要する時間がどの程度変わるのかを見てみます。

	conv5	conv4	conv3
訓練可能パラメータ数	8,931,328 (37.86%)	20,569,600 (87.20%)	22,927,104 (97.20%)
1epochの所要時間	44秒	70秒	93秒

特にパラメータ数に関してconv5からconv4に変えるだけで劇的に変わります。
conv3に至っては、ほとんど全部のパラメータが再訓練されると言っても過言ではありません。
これでResNet50の既存の学習成果を活かせるのか、少々不安ではあります。

また、1epochの所要時間に関しては、パラメータ数ほどの変化はありませんが、やはり時間が掛かるようにはなっています。

では、結果に関しても見てみましょう。

まずは、いつものように学習用データ内での最短距離の分布から。

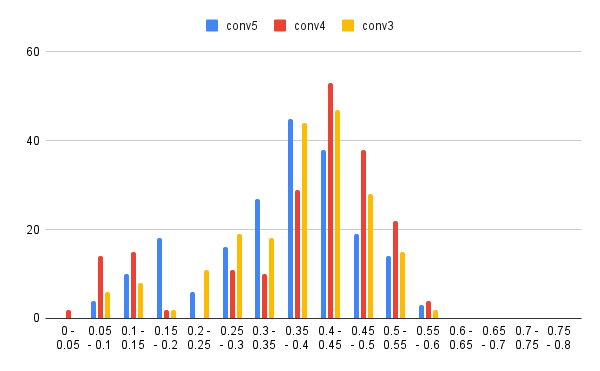
特に重要な0.2未満の状況を確認しやすいように累積の折れ線グラフとしてプロットしてみます。

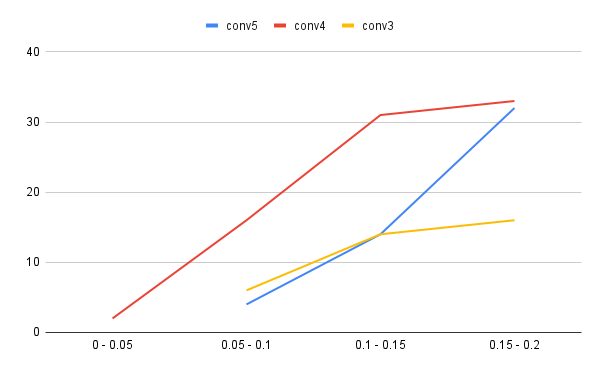
conv4の状況が少々謎ですが、conv3の方は良さそうですね。

テストデータに関するポジティブ、ネガティブの分布状況に関しても見てみましょう。

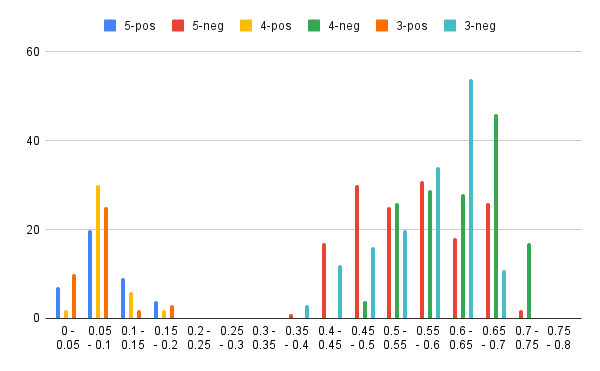
なんか、グラフ化すると逆に比較しづらくなってきている印象が…
もっと変化が大きければ、グラフでの比較も有効なんですが。

と言うことで、素データを見てみましょう。

	5-pos	5-neg	4-pos	4-neg	3-pos	3-neg
0 – 0.05	7		2		10
0.05 – 0.1	20		30		25
0.1 – 0.15	9		6		2
0.15 – 0.2	4		2		3
0.2 – 0.25
0.25 – 0.3
0.3 – 0.35
0.35 – 0.4		1				3
0.4 – 0.45		17		4		12
0.45 – 0.5		30		26		16
0.5 – 0.55		25		29		20
0.55 – 0.6		31		28		34
0.6 – 0.65		18		46		54
0.65 – 0.7		26		17		11
0.7 – 0.75		2
0.75 – 0.8

特筆すべきは0.1〜0.2に含まれる数です。
conv3が最も少なく、合計で5件となっていますが、内訳を見ると問題児である35に絡むものが4件あるため、実質的には1件と考えても良いかもしれません。

ポイントとなる距離に関しても見てみます。

	conv5	conv4	conv3
ポジティブ最小	0.02668554 (41-42)	0.04106394 (21-25)	0.03965018 (21-25)
ポジティブ最大	0.19334004 (32-35)	0.16469733 (34-35)	0.19634458 (31-35)
ポジティブ最大（35以外）	0.15223585 (32-33)	0.13041656 (23-24)	0.11376911 (23-24)
ネガティブ最小	0.38812259 (35-45)	0.47761598 (24-45)	0.36387824 (24-45)

前述したように、conv3におけるポジティブの実質的な最大距離は23-24間の0.1137…であり、この1例を除けば、ポジティブとの距離は0.1未満に納まっていると言うことになります。
23-24間の距離も、conv5の0.1522…、conv4の0.1304…と比較して、かなり0.1に近づいてきていますし、もう少し精度を上げれば、0.1をポジティブ判定の閾値にできるかもしれません。

なお、23,24は以下の画像になります。

一方、今まで35を除いたポジティブ最大距離であった32,33は以下の画像です。

見た目の印象としては、現状のように23,24の方が違いが大きいと判断されて然るべきかと思います。

なお、1回の学習結果では「まぐれ」と言うこともありますので、とりあえず3回同じ条件で学習を実行してみました。

結果は以下の通り。

	3-1-pos	3-1-neg	3-2-pos	3-2-neg	3-3-pos	3-3-neg
0 – 0.05	10		14		7
0.05 – 0.1	25		21		28
0.1 – 0.15	2		3		2
0.15 – 0.2	3		2		3
0.2 – 0.25
0.25 – 0.3
0.3 – 0.35
0.35 – 0.4		3		3
0.4 – 0.45		12		13		9
0.45 – 0.5		16		14		16
0.5 – 0.55		20		7		17
0.55 – 0.6		34		10		33
0.6 – 0.65		54		56		60
0.65 – 0.7		11		44		15
0.7 – 0.75				3
0.75 – 0.8

少なくとも今回の3回の学習においては、「35を除いたポジティブ最大距離は1例を除いて0.1未満に納まる」と言う仮説は全てのケースに当てはまるものでした。

問題の23-24の距離に関しても、以下に示すように、概ね安定的に0.12弱辺りで推移しています。

1回目	2回目	3回目
0.11376911	0.11845265	0.11792170

上記より、現時点の方向性としては「0.1を閾値としてポジティブ判定したい」と言うことになるのですが、そうなると、逆に0.1未満となるネガティブの存在が気になります。

前述した3回の学習モデルに関して、学習用データにおけるアンカーとネガティブの最短距離が0.1未満となるケースを抽出してみました。
結果は以下の通り（距離の近い順です）。

1回目

		0.06439417882861764
		0.07739744282341943
		0.09873673945958461

2回目

		0.06796833670233304
		0.07691429669857208
		0.09870319560126051
		0.09941481881627623

3回目

		0.0618521343779298
		0.08186588318279953
		0.09682036600345434

ラインナップには若干の変動がありつつも、結局は上記4組に限定されるようです。
特に最初の2組は固定です。
一方で、残り2組に関しては、いずれも0.096以上の距離がありますし、モデルによっては0.1以上と判断しているケースもあるので、もう少し精度が向上すれば0.1未満グループから除外できるかもしれません。

最も距離が近いと判断されている1組目の画像ですが、前回の高難易度トップ5には入ってこなかったものです。
人間が判断すれば、ラベルの微妙な色の違いと、印字されている文字の違いで区別できるのですが、今回ポジティブのデータ拡張に色相操作を加えたことで、逆に判別における色の重要度が下がってしまい、結果的に距離が縮まってしまった可能性があります。
ただ、見方を変えれば、学習方法の調整で対処できる可能性があるとも言えます。

2組目の画像は前回もNo.2に君臨していたもので、この画像辺りが現在の学習用データ内での最難関と言えるのかもしれません。

一方で、前回のNo.1であった下記組み合わせですが、今回は登場しませんでした。

上記組み合わせに関する今回の3回の距離計測結果を示すと、以下のようになっています。

1回目	2回目	3回目
0.28356758160204665	0.24892885170892887	0.27291517903442364

前回も言及したように、上記組み合わせは人間が見ても判別が難しいと思うのですが、今回は予想以上に距離が大きくなっていました。
どうやって違いを判別しているのでしょう？
この判別ができるのであれば、今回のNo.1,2辺りも文字の違いで区別できそうな気がするのですが？

まとめ

色々と施策を実行しましたが、訓練可能レイヤの調整は、かなり有効そうな印象があります。
実は「conv2_block1_out」に関しても試してみたのですが、逆に精度が大きく劣化したので、現時点では「conv3_block1_out」が最適解と判断しています。

検証データの固定化も、学習の推移を観察する上で、相当に効果的です。
やはり、深層学習における学習データの選択って最重要課題ですね。

一方で、色相操作辺りは諸刃の剣と言ったところでしょうか。
同じラベルが少し違った色合いに見えるケース（ポジティブ判定）と、色の違いでラベルを区別するケース（ネガティブ判定）の、どちらも考慮した、程良いバランスの学習が果たして可能であるのか？
なかなか難しそうな印象があります。

透視変換の実施も、学習データの多様性を向上させる点には貢献していると思うのですが、成果に繋がっているかという点に関しては微妙です。
とは言え、少なくとも結果を悪くしている印象はないので、拡大・縮小＋移動の発展形として、この方式は今後も採用していきたいと思います。

いずれにしても、なんとなく0.1辺りを閾値としてポジティブ（一致）判定ができそうな予感がしてきました（あくまで予感レベルですが）。
もう少し精度向上を目指したいところですが、少々手詰まり気味です。
やはり現状の学習用データ（異なるラベルの画像群）とデータ拡張だけでは、適切な距離学習を行うには少々無理があるのかもしれません。

と言うことで、そろそろ学習用データの追加（I君再召喚）も視野に入れながら、今後の方向性を探っていきたいと思います。