前回の投稿(【ワイン画像識別2026】今更ながらPyTorch)では、TensorFlow/KerasからPyTorchにフレームワークを変更した件に関して書きましたが、そのような作業が必要になった根本的な理由は、ベースモデルの変更が必要になったことにあります。
それまで使用してきたベースモデル(EfficientNetV2L)の能力では目的(ラベル画像によるワイン識別)を達成することは難しそうな気配が出てきたためモデルの変更を考えたのですが、期待したモデルがMac(Apple Silicon)上のTensorFlowでは動作しなかったことに端を発し、紆余曲折を経てPyTorchへの全面書き換えに至った訳です。
と言うことで、改めて新モデル(DINOv2)での学習を開始したのですが…精度が全然上がりませんでした。orz
まず、根本的な問題として、DINOv2はEfficientNetV2Lと比較して、メモリ消費量が大きいです。
これは、入力解像度が384×384(EfficientNetV2L)から518×518(DINOv2)に拡張されたことと、アーキテクチャとしてCNN(EfficientNetV2L)よりもViT(DINOv2)の方が多くのメモリを必要とすることに起因するようです。
上記への対処として、バッチサイズを小さくしたり、訓練可能な(パラメータ変更可能な)層を減らすなどの調整を行うしかなかったのですが、これらの影響もあってか、F1/Fβスコア等の数値がEfficientNetV2Lと比較して、全く及ばない状況が続きました。
この辺のことをAI先生に相談させてもらったところ、以下の2点で改善の余地があるのではないかとの話になりました。
- DINOv2は完成度の高いモデルであり、このモデルを少ない訓練データと貧素な開発環境で書き換えようとすることが、そもそもの間違い。
よって、DINOv2自体には変更を加えず、一部の層に新規に追加した少量のパラメータに対して変更を行う方式(構造)を採用すべし。 - トリプレット学習はハードサンプルを適切かつ十分に用意することが必要で、加えてバッチ内のトリプレットの組み合わせが成果に大きく関係する。
バッチサイズが小さくなれば、当然ながら学習の精度が落ちる。
また、学習に際して3つのデータ(アンカー・ポジティブ・ネガティブ)を扱うため、その分多くのメモリを必要とする。
これを少ない訓練データと貧素な開発環境で実施しようとすることが、そもそもの間違い。
よって、学習時のデータ選択に制約が少なく、メモリ効率の良い学習方法を採用すべし。
と言うことで、採用されたのが LoRA と ArcFace でした。
LoRA(Low-Rank Adaptation)
LoRAが何者であるかを理解する前に、「PEFT」という概念を理解しておくべきかと思います。
PEFT(Parameter-Efficient Fine-Tuning)
「巨大なモデルの大部分を凍結(Freeze)し、ごく一部のパラメータだけを学習させることで、効率的に特定のタスクへ適応させる技術」の総称つまり、今まで実施してきた手法も一部の層のパラメータを更新する方法であったため、「PEFT」であったと言えます。
ただ、今までの手法がベースモデル自身のパラメータを更新していたのに対し、LoRAではベースモデルのパラメータは変更せず、学習結果を反映するための(あくまでベースモデルのパラメータ量と比較して)少量のパラメータを追加&更新することで、効率的に学習を行おうとするものです。
この辺の解説は、例によってAI先生にお願いしましょう。
LoRAは、学習済みの巨大なモデル(ベースモデル)に対して、以下のプロセスで効率的な微調整を行います。
1. 重みの凍結と追加
ベースモデルが持つ元の重み(行列W)はすべて凍結し、学習中も一切変更しません。
その代わりに、特定の層に対して新しく2つの低ランク行列AとBを追加します。
2. 行列AとBの構造(次元の整合性)
対象となる層の重み行列Wがn*m次である場合、追加する行列は以下のサイズを持ちます。
行列A: n*r次
行列B: r*m次
ここでr(ランク)は、元の次元よりも遥かに小さい値(例:8や16)に設定されます。
3. 学習の対象
学習(チューニング)の対象は、この新しく追加された行列AとBのパラメータのみです。
その総数は (n+m)*r です。
ベースモデルの巨大なパラメータ群は動かさないため、計算コストとメモリ消費を劇的に抑えることが可能です。
4. 重みの補正メカニズム
学習によって最適化された行列AとBの積(A*B)を計算すると、行列の積の性質により、元の重みと同じn*m次の行列が得られます。
計算式: W_updated = W_frozen + (A*B)
この積(A*B)が、ベースモデルの重みに対する「差分(補正値)」として機能します。
元の知識を保持したまま、特定のタスク(ワインラベル識別など)に必要な補正をピンポイントで加えることで、モデルの挙動を精密にコントロールします。ポイントであるパラメータ数ですが、対象となる層のパラメータの構造が1,000*1,000であった場合、パラメータ総数は1,000,000ということになりますが、LoRAでは(1,000+1,000)*r となるため、例えば r=8 でも16,000であり、非常に少量のパラメータで学習が実現できることになります(ただし、パラメータ数の比が、そのまま計算コストやメモリ消費量の削減率になる訳ではないようですが)。
A,B行列の限られたパラメータを更新し、その演算結果でベースモデルの重みを補正するだけで、何故モデルの挙動が「精密に」コントロールできるのかは謎ですが、この辺は深みにハマりそうなので追求はしないでおきます。
なお、実際の実装においては、LoRAの派生系である「DoRA (Weight-Decomposed Low-Rank Adaptation)」を使用しています。
DoRAに関する解説は以下の通り。
DoRAは、重みを「向き(Magnitude)」と「大きさ(Direction)」に分解して学習します。
LoRAは主に「向き」の変化を捉えますが、DoRAはこれらを個別に最適化することで、フルファインチューニングの挙動に極めて近い学習能力を発揮します。
オリジナルLoRAよりも少ないrで高い精度が出せることが多く、「微細な模様の差」を学習する際に非常に強力です。原理は良くわかりませんが、LoRAオリジナルよりも高い精度が出せそうだと言うことは、何となく伝わってきます。
ArcFace
トリプレット学習が「アンカー・ネガティブ間の距離を、アンカー・ポジティブ間の距離よりも一定量(マージン)以上遠ざける」という「サンプル間の相対距離」の最適化を目的とした学習であったのに対し、ArcFaceはクラス(同じラベルの画像の集まり)に対して「代表ベクトル」という目標を設け、同クラスのベクトル(エンベディング結果)が代表ベクトルに近づくようにしつつ、異なるクラスの代表ベクトルは相互に遠ざけるように学習を行う方式です。
本来の学習対象はあくまで「特徴抽出器」(DINOv2 + DoRA + Projection Head)ですが、学習の手段として「分類器」(ArcFace)を追加し、最終的なクラス分類の精度(つまり入力されたデータを正しいクラスに分類する際の確度)を向上させるように学習を進めます。
ArcFaceのパラメータは、当該学習で扱うクラス数をm、特徴抽出器が出力するベクトルの次元数をnとすると、m * n の行列です(これを「重み行列W」と呼称します)。
実は、重み行列Wの各行は特定のクラスの「代表ベクトル」(つまり目指すべき収束先)となっていて、それ故に重み行列Wの列数は特徴抽出器が出力するベクトルの次元数と同じ(n)で、それがクラス数(m)行並んでいる構造を持つ訳です。
なお、ArcFaceにおいては、代表ベクトルを含む各ベクトルは正規化されており、つまりはn次元における半径1の超球面上のどこかを指すようなベクトルになっているイメージです。
この状況では、2つのベクトルの遠近は、両者のなす角の大小と等価です。
学習の初期段階では、重み行列Wの内容、つまりは各クラスの代表ベクトルはランダムな値で構成されているようですが、学習が進むにつれて適正な方向(同クラスに属する各ベクトルの中心として適当で、かつ異なるクラスの代表ベクトルとは十分離れた方向)を向くように調整されます。
その代表ベクトルに対して各クラスのベクトルが近づくように特徴抽出器に学習させることが、ArcFace学習の本質と言えます。
なお、前述したような学習がどのように行われるかを理解するためには、やはり損失関数を理解する必要があります。
ArcFaceの損失関数は以下のような式になっています。
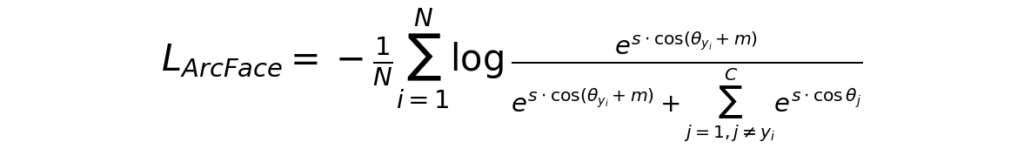
複雑なので、まずは全体像を整理したいと思います。
Nは損失計算を行う際の対象データの数であり、つまりはバッチサイズです。
よって、最初の (1/N)Σ の部分はバッチ内の各データに関する「損失」の算術平均を計算しているだけです。
符号(マイナス)の位置がややこしいですが、算術平均の要素となる各データの「損失」が -log(…) なる式で表されています。
logの中身(真数)に関しても、細かく見ていきましょう。
一旦 m を無視すると、分子・分母を構成する各項は exp(s*cos(θ)) という式で表されています。
θはデータ(i)のベクトルと各クラスの代表ベクトル(j)がなす角であり、当該データが属するクラスの代表ベクトル(正解ベクトル)に関してはj=yiで示しています。
分母に関しては、正解ベクトルに関する exp(s*cos(θ)) の値と、それ以外の代表ベクトルとの exp(s*cos(θ)) の合算結果を足しているだけなので、つまりはデータ(i)と全代表ベクトルに関する exp(s*cos(θ)) の合計になります。
よって、s*cos(θ) を省略すると、logの真数部分は exp() / Σexp() なる構造であることが分かります。
これは Softmax と呼ばれる式です。
Softmaxの解説は以下の通り。
ソフトマックス関数とは、複数の数値(スコア)を「合計が1(100%)になる確率」へと変換する仕組みです。
大きな特徴は、各数値をそのまま割合にするのではなく、指数関数を用いて差を強調する点にあります。これにより、最も大きな値がより際立ち、マイナスの値も正の確率として扱えるようになります。AIが「これは猫である確率が90%」といった最終的な予測結果を出す際や、注目すべき要素を抽出する計算で不可欠な技術です。上記で言う「スコア」は、今回のケースでは cos(θ) と考えて良いでしょう。
cos(θ) はデータ(i)と代表ベクトルとのコサイン類似度(1 〜 -1)であり、これはデータ(i)が各クラスに属する可能性を「近さ」として示した数値です。
このことから、logの真数部分は「入力データが、正解クラスの代表ベクトルとどれだけ似ているか(類似度)に基づき、Softmaxによって算出された『正解クラスである確率(確度)』」と言えます。
なお、cos(θ) の値の範囲は 1 〜 -1 と非常に狭いため、このままでは cos(θ) の変化が確率(確度)に与える影響が小さくなってしまいます。
よって、係数 s を掛けることによって変化を増幅して、確率(確度)も大きく変動するように操作している訳です。
この係数 s のことを「スケールファクタ」と呼ぶようで、通常は 30 〜 64 程度の値とするようです。
上記より、Softmax部分は『正解クラスである確率(確度)』であることが分かりましたが、これはあくまで確率(確度)であり、正解(100%=1.0)から不正解(極めて0に近い値)までを示すことになります。
しかし、今回必要となる値は「損失」であり、正解(確度100%)を0とし、確度が下がるほど大きな値となるように変換したい訳です。
この計算が -log になります。
以上の内容を簡単にまとめると、ArcFaceにおける損失計算の流れは、以下のストーリーで成り立っていると言えます。
- 類似度(Cos)を出す: 「どのくらい似ているか」を測る。
- Softmaxを通す: 全体の中での「正解クラスである確率」に変換する。
- -logをとる: その確率が低いほど巨大な「損失」となるよう数値化する。
- 算術平均をとる:バッチとしての「損失」を数値化する。
最後に、今まで無視してきた m の存在に触れていきます。
実は、この m(マージン)こそがArcFaceの特徴で「正解クラスと判定されるための合格基準を、角度(方向)の面で意図的に厳しくするペナルティ」です。
先に示した式にあるように、マージンは正解クラスとのコサイン類似度の計算時にのみ使用されます。
この結果、正解クラスとのコサイン類似度はマージン分だけ本来の値より悪くなります。
大雑把な例えとしては「100点満点中90点取れているにも関わらず、無理やり20点減点して70点しか取れていないように見せかけている」と言ったところでしょうか。
その上で、「もっと勉強しろ」と発破をかける訳です。
なかなか酷い話です。
上記でArcFaceの損失関数の構造的な意味を理解できたかと思いますが、改めてSoftmax部分を見ると、その値(正解確度)を増減させる要因は以下の2点です。
- データ(i)のベクトルと当該クラスの代表ベクトルとの距離の近さ(分子の大きさに影響)
- データ(i)のベクトルと他のクラスの代表ベクトルとの距離の遠さ(分母の大きさに影響)
つまり、損失を小さくするためにはデータ(i)のベクトルを当該クラスの代表ベクトルに近づけると同時に、他のクラスの代表ベクトルから遠ざける必要が生じます。
この作用により、特徴抽出器が出力する特徴量(ベクトル)が、同じクラスで集まり、違うクラスとは離れるように訓練されていく訳です。
上記内容を踏まえつつ、改めてトリプレット学習とArcFace学習の違いを見てみましょう(AI先生まとめ)。
| トリプレット学習 | ArcFace学習 | |
| 学習の基本原理 | サンプル間の相対距離を最適化 Anchor, Positive, Negativeの3点比較 | クラス代表ベクトルとの角度を最適化 全クラスとの同時比較 |
| 比較対象 | バッチ内の特定の「画像」同士 | 画像 x と「クラス重心(重み W)」 |
| メモリ効率 | 低い 有効なペアを作るために巨大なバッチが必要 | 高い 実バッチ1でも全クラスと対峙できる |
| サンプリング | 必須 (Hard Negative Mining) 似た画像を探す処理が非常に面倒 | 不要 重み行列 W が全クラスの情報を保持している |
| 学習の安定性 | 低い 崩壊しやすく、調整が難しい | 高い 収束が速く、非常に安定している |
トリプレット学習においては、トリプレット(アンカー・ポジティブ・ネガティブ)を構成するデータを適正(適した難易度)になるよう選択することや、バッチ内のトリプレットの多様性を確保することが精度に大きく影響することが体験的にも分かっています。
ArcFaceでは上記のような操作が必要ないため、その点では精度を安定的に向上させやすい方式であると思います。
また、ArcFaceは精度の面でバッチサイズの影響を受けにくいため、バッチサイズを小さくできます(処理速度には影響があるようですが)。
各種ハイパーパラメータの調整においてメモリ消費量が厳しくなってきた際に、その皺寄せをバッチサイズで解決できる点は、かなり便利です。
しかし、トリプレット学習を提案したのもAI先生だったのですが、上記を見る限り、気持ちが良い程のディスりっぷりです。
だったら、最初からArcFaceを薦めてくれればと思うのですが…
まとめ
今回は、新モデル(DINOv2)での学習に向けて新たに採用したLoRAとArcFaceに関して書いてみました。
LoRAは学習内容(パラメータの変更内容)を効率的に管理する方法、ArcFaceはデータの選択方法や組み合わせを気にする必要がなく、メモリ効率的にも優れた学習方法と言ったところでしょうか。
これら技術はDINOv2だから、あるいはViTだから有効と言う訳ではなく、ResNet50やEfficientNetV2LなどのCNN系モデルとも組み合わせ可能らしいです。
繰り返しになりますが、もっと早く教えてくれていれば…と思いますが。
なお、今までの投稿の流儀からすれば、LoRAやArcFaceと言った周辺機能ではなく、最も重要性の高いベースモデル(DINOv2)の話を真っ先にしてきたかと思います。
なぜ、そうしないのか?
それは、DINOv2が全然使い物になっていないからです。
これはDINOv2が悪いということではなく、ワイン画像識別という目的との相性や、用意できるデータ量、開発環境のスペックなど様々な要因によるものかと思っています。
いずれにしても、現在の状況ではDINOv2を育てることは難しいと判断せざるを得ません。
と言うことで、次回は早くも次のベースモデルとして選定した「SigLIP2」の紹介をさせてもらう予定です。
