「ラベル画像のトリミング(5)」では学習率を調整することでval_lossを0.025辺りまで下げることができましたが、それ以上の精度向上が難しい状況になっていました。
実は以前より、Gemini先生には精度向上のための最優先課題として「データ拡張」の導入を「強く推奨」されていました。
データ拡張とは「既存の学習用データセットに人工的なバリエーションを加えることで、モデルの汎化能力を向上させる手法」とのことで、要は手持ちの画像およびアノテーション結果に様々な変換(拡大縮小・回転・反転・色調変換など)を行うことでデータ数を水増ししようとするものです。
方向性としては理解できるものの、それはそれで面倒な作業なのだろうと避けてきたのですが、他に適当な策も無くなってきたので、いよいよ年貢の納め時と言うことで、今回はデータ拡張にチャレンジです。
なお、画像とアノテーション結果の1組のデータに関してしばしば言及することになりますので、今後も含めてこの1組のセットを「画像マスクペア」と表現します(Gemini先生によれば、英語圏でも「image-mask pair」と表現されているようなので)。
データ拡張
まず、水増し作業を手動で行うのはかなり面倒なので、何か良い方法はないものかとGemini先生に相談したところ、なんとプログラム的にできちゃうみたいです。
しかも、かなり簡単に。
心配して損しました。
具体的には「imgaug」なるパッケージを使用するらしいです。
「img」を「aug(ment)」つまり増やすと言うことですね。
早速インストールしてみます。
# pip install imgaug上記パッケージを使って、以前作成した学習用データセット生成処理「create_dataset」にデータ拡張の機能を実装してみます。
当然の如く、実装はGemini先生任せです。
結果は以下の通り。
import numpy as np
import os
import cv2
import imgaug as ia
from imgaug import augmenters as iaa
from imgaug.augmentables.segmaps import SegmentationMapsOnImage
def create_dataset(image_dir, json_dir, output_dir, original_image_size, target_image_size,
num_augmentations_per_image=5):
output_images_dir = os.path.join(output_dir, 'images')
output_masks_dir = os.path.join(output_dir, 'masks')
os.makedirs(output_images_dir, exist_ok=True)
os.makedirs(output_masks_dir, exist_ok=True)
seq = iaa.Sequential([
iaa.Fliplr(0.5),
iaa.Flipud(0.2),
iaa.Affine(
scale={"x": (0.8, 1.2), "y": (0.8, 1.2)},
translate_percent={"x": (-0.1, 0.1), "y": (-0.1, 0.1)},
rotate=(-15, 15),
shear=(-8, 8),
cval=(0, 255),
mode=ia.ALL
),
iaa.Sometimes(0.5,
iaa.GaussianBlur(sigma=(0, 1.0))
),
iaa.LinearContrast((0.75, 1.5)),
iaa.AdditiveGaussianNoise(loc=0, scale=(0.0, 0.05*255), per_channel=0.5),
iaa.Multiply((0.8, 1.2), per_channel=0.2),
], random_order=True)
image_files = os.listdir(image_dir)
for image_file in image_files:
if image_file.lower().endswith(('.jpg', '.jpeg', '.png')):
base_name = os.path.splitext(image_file)[0]
image_path = os.path.join(image_dir, image_file)
json_file_name = base_name + '.json'
json_path = os.path.join(json_dir, json_file_name)
if os.path.exists(json_path):
image = cv2.imread(image_path)
image_resized = cv2.resize(image, target_image_size)
mask = create_mask_from_json(json_path, original_image_size, target_image_size)
mask_expanded = np.expand_dims(mask, axis=-1)
cv2.imwrite(os.path.join(output_images_dir, f"{base_name}_aug000.png"), image_resized)
cv2.imwrite(os.path.join(output_masks_dir, f"{base_name}_aug000.png"), mask_expanded)
for i in range(num_augmentations_per_image):
seq_det = seq.to_deterministic()
image_aug = seq_det.augment_image(image_resized)
segmap = SegmentationMapsOnImage(mask_expanded, shape=mask_expanded.shape)
segmap_aug = seq_det.augment_segmentation_maps([segmap])[0]
mask_aug = segmap_aug.get_arr()
if mask_aug.ndim == 2:
mask_aug = np.expand_dims(mask_aug, axis=-1)
mask_aug_255 = mask_aug.astype(np.uint8)
cv2.imwrite(os.path.join(output_images_dir, f"{base_name}_aug{i+1:03d}.png"),
image_aug)
cv2.imwrite(os.path.join(output_masks_dir, f"{base_name}_aug{i+1:03d}.png"),
mask_aug_255)関係箇所を個別に見ていきましょう。
変換内容の定義
以下の箇所で変換内容の定義(設定)を行っています。
seq = iaa.Sequential([
iaa.Fliplr(0.5),
iaa.Flipud(0.2),
iaa.Affine(
scale={"x": (0.8, 1.2), "y": (0.8, 1.2)},
translate_percent={"x": (-0.1, 0.1), "y": (-0.1, 0.1)},
rotate=(-15, 15),
shear=(-8, 8),
cval=(0, 255),
mode=ia.ALL
),
iaa.Sometimes(0.5,
iaa.GaussianBlur(sigma=(0, 1.0))
),
iaa.LinearContrast((0.75, 1.5)),
iaa.AdditiveGaussianNoise(loc=0, scale=(0.0, 0.05*255), per_channel=0.5),
iaa.Multiply((0.8, 1.2), per_channel=0.2),
], random_order=True)まず、全体的には以下の構造になっています。
iaa.Sequential([...], random_order=True)第一引数の配列には具体的な変換処理を羅列しています。
ここで指定された変換処理はパイプライン実行されるようですが、第二引数の「random_order=True」指定により、パイプラインにおける変換処理の実行順序がランダムになるようです。
つまり、データ拡張における変換は複数の変換の組み合わせで行われ、かつ個別の変換の実行順序も変化するため、生成されるデータの多様性が向上すると言うことのようです。
では、変換処理を個別に見ていきます。
iaa.Fliplr(0.5)画像を左右に反転します。
引数は実行する確率で、0.5は50%を意味します。
iaa.Flipud(0.2)画像を上下に反転します。
引数は実行する確率で、0.2は20%を意味します。
iaa.Affine(
scale={"x": (0.8, 1.2), "y": (0.8, 1.2)},
translate_percent={"x": (-0.1, 0.1), "y": (-0.1, 0.1)},
rotate=(-15, 15),
shear=(-8, 8),
cval=(0, 255),
mode=ia.ALL
)画像をアフィン変換します。
「scale={“x”: (0.8, 1.2), “y”: (0.8, 1.2)}」は拡大縮小で、「(0.8, 1.2)」は元のサイズの80%から120%の間でランダムに拡大縮小することを意味します。
「translate_percent={“x”: (-0.1, 0.1), “y”: (-0.1, 0.1)}」は平行移動で、「(-0.1, 0.1)」は画像の幅(または高さ)の-10%から+10%の間でランダムに移動すること意味します。
「rotate=(-15, 15)」は回転で、「(-15, 15)」は-15度から+15度の間でランダムに回転することを意味します。
「shear=(-8, 8)」はシアー(せん断)変換で、大雑把に言えば長方形の元画像を平行四辺形に変換します。「(-8, 8)」は傾ける角度を-8度から+8度の間でランダムに選択することを意味します。
「cval=(0, 255)」は変換によって生じる画像の範囲外の部分を埋める「色」の指定で、「(0, 255)」は0(黒)から255(白)の間のランダムな値で埋めることを意味します。
「mode=ia.ALL」は画像の範囲外の部分を埋める「方法」の指定で、「ia.ALL」はmodeとして選択できる「constant」「edge」「symmetric」「reflect」「wrap」をランダムで適用することを意味するようです。なお、「constant」は特定の色で埋めることを意味するようで、modeが「constant」の場合のみ前述のcvalで指定された色が適用されるようです(その他のモードに関しては話が長くなりそうなので追求せず)。
iaa.Sometimes(0.5,
iaa.GaussianBlur(sigma=(0, 1.0))
)まず、Sometimesは第一引数で指定された確率で第二引数で指定された変換を実行することを意味します。
変換として指定されている「 iaa.GaussianBlur(sigma=(0, 1.0))」は「ガウスぼかし」で、「sigma=(0, 1.0)」はぼかしの強さを示すシグマ値が0(ぼかしなし)から1.0の間でランダムに選択されることを意味します。
まとめると、0.5(50%)の確率で、シグマ値が0から1.0の間のランダムな値でのガウスぼかしを実行すると言うことです。
iaa.LinearContrast((0.75, 1.5))画像のコントラストを調整します。
「(0.75, 1.5)」は元のコントラストの75%から150%の間でランダムに調整されることを意味します。
iaa.AdditiveGaussianNoise(loc=0, scale=(0.0, 0.05*255), per_channel=0.5)画像にガウスノイズを追加します。
引数に関しては…何か難しい話のようなので説明は割愛。
iaa.Multiply((0.8, 1.2), per_channel=0.2)画像の輝度を調整します。
「(0.8, 1.2)」は各ピクセル値を元の値の80%から120%の間でランダムに乗算することを意味します。これにより、画像が暗くなったり明るくなったりします。
「per_channel=0.2」は20%の確率で、各チャネル(R, G, B)に独立した乗数を適用することを意味します。残りの80%では、すべてのチャネルに同じ乗数が適用されます。
変換の実行
前述したように、変換内容に関しては相当数のランダム要素があります。
しかし、ここで注意が必要なのは、画像マスクペアを構成する画像とマスク(アノテーション結果)に対しては全く同じ変換を行う必要があると言う点です。
もし、画像とマスクに違う変換を行ってしまうと、マスクが画像上のラベルの位置を正しく表現できていない状態になってしまいます。
蛇足ながら、1つの画像マスクペアに対して異なる変換を行い、複数の変換結果を生成することは問題ありません。
当然ながら、異なる画像マスクペアに対して異なる変換を行うことも問題ありません。
と言うことで、以下の処理を実行することで、ランダム要素が決定(固定)された、新たなオブジェクト「seq_det」を生成しています。
seq_det = seq.to_deterministic()上記seq_detを画像マスクペアを構成する画像とマスクの両方に対して共通的に利用することで、両者に差異なく変換が適用できるようになります。
image_aug = seq_det.augment_image(image_resized)先にランダム要素を固定化した変換を画像に対して実行しています。
segmap = SegmentationMapsOnImage(mask_expanded, shape=mask_expanded.shape)mask_expandは(若干の追加加工をしていますが)大雑把に言えば、LabelMeのアノテーション結果(対象範囲を示すポリゴンを構成する各ポイントの座標情報)から、対象部分のピクセルの値は255、対象外の部分は0となる画像相当のデータ(型はNumPy配列)です。
それを、imgaugが処理に使用できるオブジェクトに変換しています。
segmap_aug = seq_det.augment_segmentation_maps([segmap])[0]先に生成したオブジェクトに対して変換を実行しています。
画像の変換結果と差異が生じないように、同じseq_detを使用している点が重要です。
画像本体とは異なり、アノテーション結果(セグメンテーションマップ)に対しては専用のメソッド「augment_segmentation_maps」を使用する必要があるようです。
augment_segmentation_mapsはリスト形式で複数の対象を入力し、それぞれに関する処理結果を同じくリスト形式で返しますが、今回はあくまで1つの対象に関する処理を行いたいだけなので、上記のように入力リストには当該対象のみを指定し、戻り値のリストにおける先頭(要素が1つしかないので)の値(オブジェクト)をsegmap_augとして取得しています。
mask_aug = segmap_aug.get_arr()先にアノテーション結果(NumPy配列)をimgaugが使用しやすいオブジェクト(segmap)に変換しましたが、今度は処理結果であるsegmap_augオブジェクトをNumPy配列に戻しています。
for i in range(num_augmentations_per_image):今まで解説してきた変換は上記for文の中で実行されています。
つまり、1組の画像マスクペアから、num_augmentations_per_imageで指定した数だけ変換が適用された別の画像マスクペアが生成されます。
なおfor文内で「seq.to_deterministic()」を実行しているので、同じ画像マスクペアから生成された画像マスクペアでも、生成ごとに内容は異なっています。
これにより異なる特徴を持つ画像マスクペアを大量に水増しできると言う訳です。
データ拡張結果
今回はnum_augmentations_per_imageを5とし、元となる画像マスクペアから追加で5組の画像マスクペアを生成しました。
以下に例を示します。
 |  |  |  |  |  |
 |  |  |  |  |  |
一番左が元画像マスクペアで以降がデータ拡張結果です。
確かに前述したような変換が複合的に適用されているようです。
検証
データ拡張により元データセット200組を1200組まで水増ししました。
それは良かったのですが、当然ながら学習に掛かる時間も6倍になりました。
今までは1epochが約30秒でしたが、データ水増し後は約180秒要するようになっています(計算的には帳尻が合っています)。
以前のように1000epochなど実行しようと思ったら、50時間掛かってしまいます。
ただ、データ数を増やしたことで、1epochでの学習効率が上がっていることは期待できるかもしれません。
と言うことで、まずは100epochくらいから試してみることにします。
検証1:固定学習率 / 100epoch
前回と同様に学習率が6.40E-05, 3.20E-05, 1.60E-05の3パターンに対して、それぞれ100epochの学習を実行してみます(これでも5時間掛かりますが)。
結果は以下の通り。
左がloss, 右がval_lossの推移です(左右で尺度が違うので要注意)。
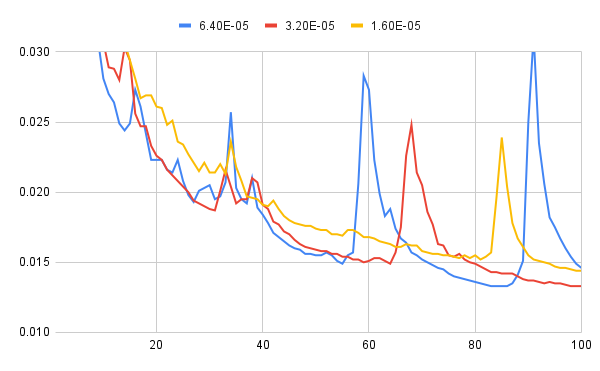
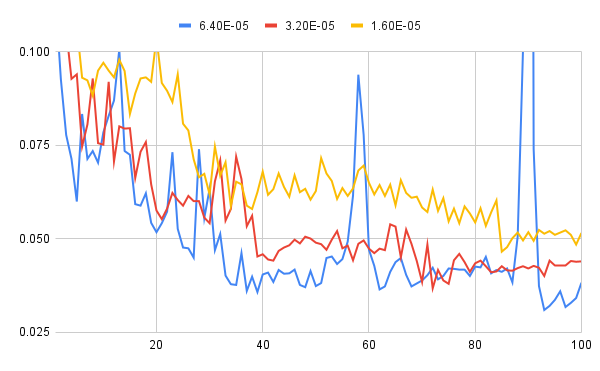
val_lossの方は例によって増減が激しいので判断が難しいですが、両者とも何となく継続して減衰傾向にあるような印象です。
もう少しepochを増やしてみましょう。
検証2:学習率減衰 / 300epoch
単純にepochを増やして先の3パターンを実行しようと思うと、検証に要する時間がどんどん増えていってしまうので、少し工夫をしてみました。
実は、これは以前も試したことがあるのですが、val_lossの値が所定のepochの間に改善しなければ、学習率を下げてみるという方法です。
具体的には以下のような関数をmodel.fitのcallbacks引数に追加します。
ReduceLROnPlateau(
monitor='val_loss',
factor=0.5,
patience=50,
verbose=1,
min_lr=1e-6
),上記で「monitor」は監視対象の指標です。ここでは当然ながら「val_loss」を指定しています。
「factor」は学習率を下げる際の係数で、0.5であることから、従来の半分に学習率を減らしていくことを意味します。
「patience」は「monitor」で指定した指標が改善しないepochがどの程度続いたら学習率を下げるかを指定するもので、ここでは50epochの間val_lossの最小値が更新されなければ学習率を下げるよう指定しています。
「verbose=1」は学習率の変更が生じた時に画面上に情報表示する指定です。具体的には以下のような表示が出ます。
Epoch 265: ReduceLROnPlateau reducing learning rate to 1.5999999959603883e-05.上記は学習率が1.60E-05相当の値に変動した際の表示です。数値が微妙に違っているのはコンピュータあるあるの小数誤差が関係するのでしょうが、今回は数値の正確性は重要ではないのでスルーします。
「min_lr」は学習率の下限です。あまり学習率が小さくなり過ぎると学習効率に悪影響なので、このような設定があるようです。
今回は初期の学習率を6.40E-05とし、50epochの間にval_lossに改善がなければ学習率を半分に減らしていく(つまりは3.20E-05, 1.60E-05, …と変化させていく)ように設定し、これを300epoch実行してみました。
結果は以下の通り。
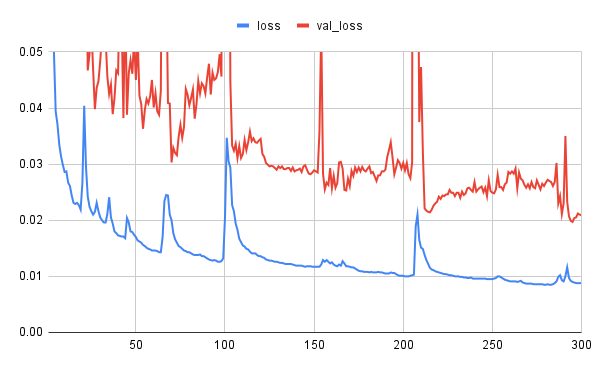
上記推移を見ると、減衰傾向は継続しているような印象です。
では、さらにepochを増やして…とも考えましたが、実は362epochにおいて学習が止まってしまうという現象が発生していて、これ以上の検証ができていません。
この現象は再現性があって、2回しか試していませんが、いずれも同じ362epochで止まっているので、メモリ不足のような環境要因とは別の理由で発生しているように思われます。
なお、300epochの学習においてval_lossが更新された際のepoch, loss, val_lossと、その際の学習率(learning_rate)に関しては以下の通り。
| epoch | loss | val_loss | learning_rate |
| 1 | 0.1944 | 0.1480 | 6.40E-05 |
| 2 | 0.0858 | 0.0893 | 6.40E-05 |
| 4 | 0.0502 | 0.0811 | 6.40E-05 |
| 5 | 0.0394 | 0.0777 | 6.40E-05 |
| 8 | 0.0314 | 0.0746 | 6.40E-05 |
| 10 | 0.0286 | 0.0640 | 6.40E-05 |
| 19 | 0.0219 | 0.0600 | 6.40E-05 |
| 21 | 0.0404 | 0.0523 | 6.40E-05 |
| 23 | 0.0242 | 0.0467 | 6.40E-05 |
| 27 | 0.0215 | 0.0398 | 6.40E-05 |
| 37 | 0.0194 | 0.0389 | 6.40E-05 |
| 43 | 0.0171 | 0.0382 | 6.40E-05 |
| 54 | 0.0156 | 0.0363 | 6.40E-05 |
| 70 | 0.0200 | 0.0303 | 6.40E-05 |
| 123 | 0.0130 | 0.0302 | 3.20E-05 |
| 124 | 0.0129 | 0.0299 | 3.20E-05 |
| 125 | 0.0128 | 0.0296 | 3.20E-05 |
| 127 | 0.0127 | 0.0296 | 3.20E-05 |
| 128 | 0.0126 | 0.0293 | 3.20E-05 |
| 129 | 0.0126 | 0.0290 | 3.20E-05 |
| 137 | 0.0122 | 0.0288 | 3.20E-05 |
| 139 | 0.0120 | 0.0287 | 3.20E-05 |
| 143 | 0.0119 | 0.0286 | 3.20E-05 |
| 147 | 0.0118 | 0.0283 | 3.20E-05 |
| 148 | 0.0118 | 0.0282 | 3.20E-05 |
| 156 | 0.0126 | 0.0255 | 3.20E-05 |
| 167 | 0.0123 | 0.0254 | 3.20E-05 |
| 168 | 0.0118 | 0.0253 | 3.20E-05 |
| 212 | 0.0138 | 0.0221 | 3.20E-05 |
| 213 | 0.0129 | 0.0217 | 3.20E-05 |
| 214 | 0.0122 | 0.0215 | 3.20E-05 |
| 215 | 0.0115 | 0.0214 | 3.20E-05 |
| 289 | 0.0093 | 0.0211 | 1.60E-05 |
| 293 | 0.0097 | 0.0207 | 1.60E-05 |
| 294 | 0.0092 | 0.0199 | 1.60E-05 |
| 295 | 0.0090 | 0.0197 | 1.60E-05 |
50epochの間val_lossが改善しないと学習率を変更することから、120epochと265epoch辺りで同変更が発生しているようです。
学習率変更後に再びval_lossの改善が見られるようになっていますが、これが学習率を下げた効果なのか、たまたまなのかは判断が難しいところです。
セグメンテーション結果
前述の各検証結果として生成されたモデルによるセグメンテーションを確認してみましょう。
その前に、例によって各モデルに関してval_lossが最小となった状況をまとめておきます。
「参考」情報として、前回の投稿で最もval_lossが小さかった、1.60E-05(データセット数200, 1000epoch)の情報も併記しておきます。
| 参考 | 6.40E-05 | 3.20E-05 | 1.60E-05 | 学習率減衰 | |
| epoch | 518/1000 | 93/100 | 72/100 | 85/100 | 295/300 |
| loss | 0.0067 | 0.0206 | 0.0177 | 0.0239 | 0.0090 |
| val_loss | 0.0249 | 0.0310 | 0.0368 | 0.0466 | 0.0197 |
「参考」と比較して、同じ学習率1.60E-05でも今回の値はloss, val_lossともに悪いですね。
ただ、先のグラフの印象でもそうでしたが、最小のval_lossを記録したタイミングが学習全体の終盤であることを考えると、今回の学習パターンに関しては、全般的に継続して改善の余地がある段階のように思われます。
一方で、「学習率減衰」の結果はかなり良いですね。
lossに関しては「参考」と比較して若干悪いですが、val_lossに関しては初の0.02切りを果たしました。
まぁ、学習時間で考えると「参考」が約8時間であるのに対し、「学習率減衰」は約15時間掛けているので、相応の成果がないと困るのですが。
上記を踏まえてセグメンテーション結果を見てみましょう。
| 元画像 | 参考 | 6.40E-05 | 3.20E-05 | 1.60E-05 | 学習率減衰 | |
| 1-1 |  |  |  |  |  |  |
| 1-2 |  |  |  |  |  |  |
| 1-3 |  |  |  |  |  |  |
| 1-4 |  |  |  |  |  |  |
| 1-5 |  |  |  |  |  |  |
| 2-1 |  |  |  |  |  |  |
| 2-2 |  |  |  |  |  |  |
| 2-3 |  |  |  |  |  |  |
| 2-4 |  |  |  |  |  |  |
| 2-5 |  |  |  |  |  |  |
| 3-1 |  |  |  |  |  |  |
| 3-2 |  |  |  |  |  |  |
| 3-3 |  |  |  |  |  |  |
| 3-4 |  |  |  |  |  |  |
| 3-5 |  |  | 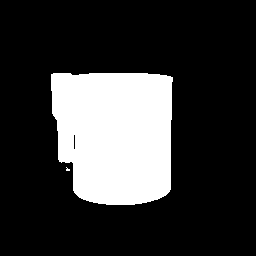 | 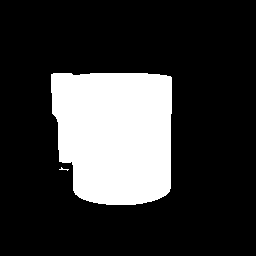 |  |  |
| 4-1 |  |  |  |  |  |  |
| 4-2 |  |  |  |  |  |  |
| 4-3 |  |  |  | 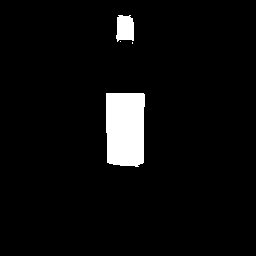 |  | 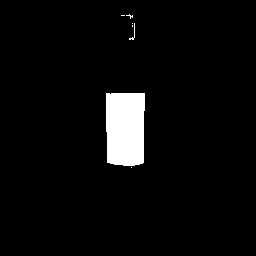 |
| 4-4 |  |  |  |  |  |  |
| 4-5 |  |  | 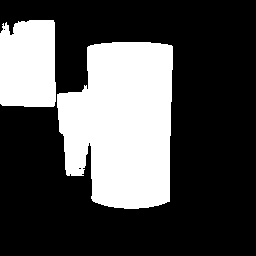 |  |  |  |
なんか、先に示した数値データと実際のセグメンテーション結果の印象が相当に違っているように思います。
前回の投稿で課題として上げた内容に関して個別に見てみましょう。
- 背景に置かれたダンボールのシールに関する誤認
「参考」の結果と比較して、全般的にかなり改善しています。
一部にはシール部分を完全に無視できているケースもあります。 - 2セット目のラベルに関する誤認(特に右上)
大写しにしたパターン(2-4)では同現象が見受けられますが、全般的に改善された印象です。 - 3-4のラベルに関する誤認
1.60E-05の結果が若干乱れていますが、その他に関してはほぼ問題ない状態です。 - キャップシールに関する誤認
6.40E-05, 3.20E-05と現象が軽減していき、1.60E-05および「学習率減衰」ではほとんど影響がありません。 - 壁の左上に描かれている何らかの図形に関する誤認
今回生成したモデルでは全く影響がありません。
上記に対して、今回のモデルで新たに生じた問題は見受けられず、少なくとも見た目の印象では「参考」の結果に対して見劣りする部分はほとんどないように思われます。
「学習率減衰」は別にしても、数値的には劣っていた6.40E-05, 3.20E-05, 1.60E-05のいずれの結果に関しても、「参考」の結果より優れて見えるのは意外です。
また、今回のモデル相互においても、数値的に優位な6.40E-05の結果よりも1.60E-05の結果の方が良いように見えます。
どうしても見た目の印象となると、大きな誤認の有無が目立ってしまい、対象部分の輪郭などがどの程度正確に認識できているか等の部分は確認しづらいので、その辺の違いかもとは思うのですが、どうにもval_lossの値の優劣と見た目の印象が合わない点には困惑します。
まとめ
数値データに関する疑問はありますが、少なくとも見た目の印象に関して言えば、今回のセグメンテーション結果はいずれもかなり満足度の高いものと言えます。
やはり、学習に使用するデータの数やバリエーションが成果に与える影響は大きいのでしょう。
ただ、これ以上データ数を増やすと学習に要する時間がどんどん増えてしまいますし、その一方で劇的な改善が望めるかと言うと、少々怪しいような気がします。
そもそも、「ラベル画像のトリミング(3)」辺りの状況と比較すると、現状でも十分精度の高いセグメンテーションができていると言っても良いのではないかと思ったりもします。
そろそろ本来の目的である「ラベル画像のベクトル検索によるワインの特定」に戻るべきかとも思いますので、何か特別に効果的と思われるセグメンテーションの精度向上施策を思いつかない限り、次回はラベル部分のトリミングからのベクトル化と検索精度の確認を行うことになるかと思います。
